How Salty is the Soup?

Let's revisit the soup example from the start from Topic 1 of this handbook. You want to know how salty the soup is, so you can either add more salt or dilute it with some water. You take your ladle and taste some soup. You decide it's not salty enough, so you add salt and keep cooking.

Not the most glamorous example, but there's a lot of important information about sampling within it.

When you scooped up some soup and tasted it, that's known as sampling. When you describe how salty the soup in your ladle is, you describe the sample using statistics.

When you used what you tasted to determine the saltiness of the entire pot of soup, that's known as an inference. You're using the sample to understand or estimate something about the entire population. When you're describing something about the entire pot of soup, you're describing the population or segment using something known as parameters.

The common notation used to describe samples and parameters are listed below for quick reference. Recognizing and reading this notation correctly can unlock more complex content about sampling outside of this handbook. A common mistake is when a new or inexperienced researcher represents their study’s sample sizes using an uppercase “N” (which represents the population or segment), instead of the lowercase “n” (which represents a sample).

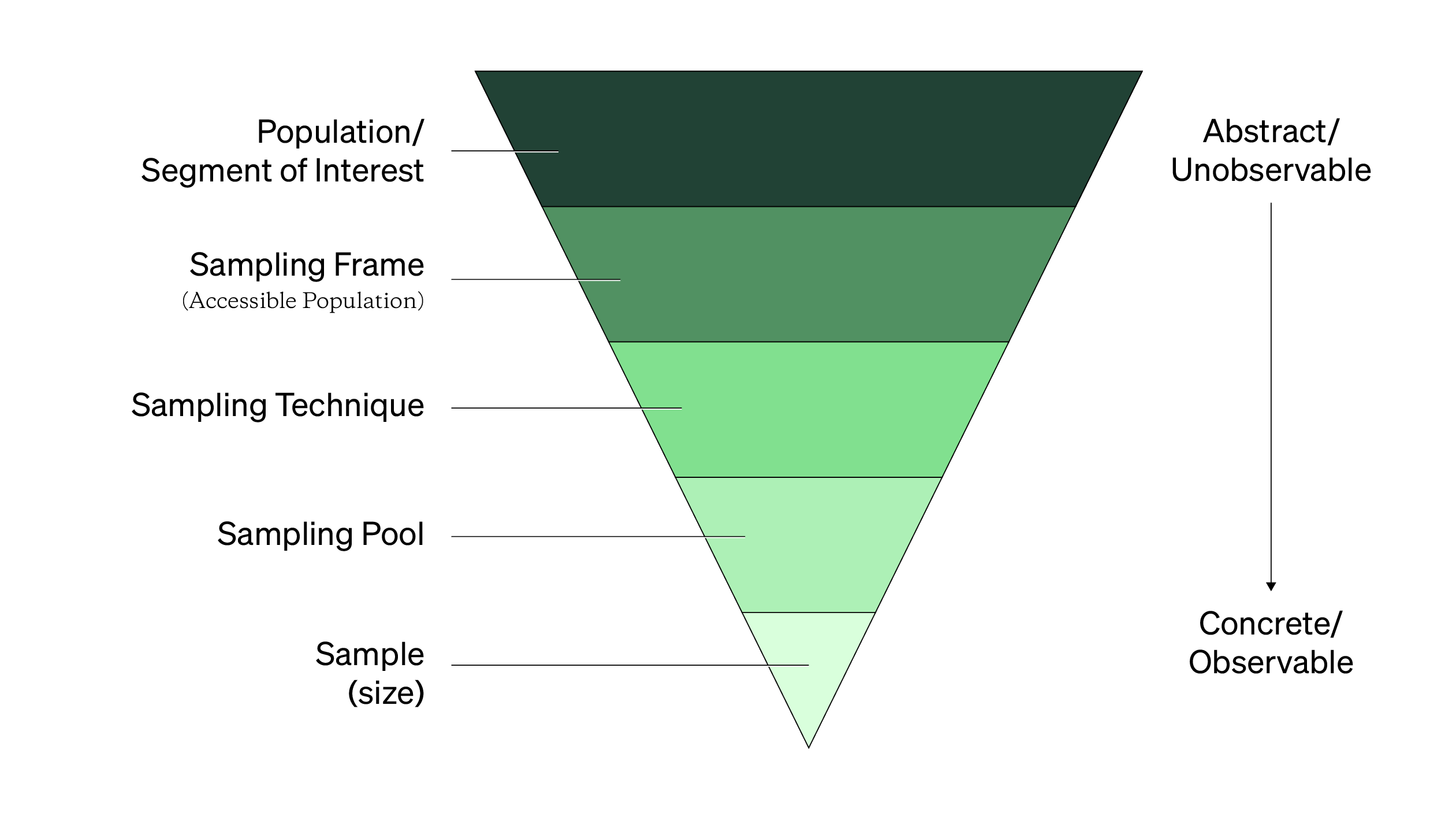
Let’s break down the steps to go from a population to a sample and back. Each step is known as a sampling stage. Each stage contains a smaller number of possible and similar participants or units that can be sampled. The focus here is a bit more on quantitative research because qualitative sampling is a bit more forgiving and flexible. Don’t worry, these ideas will help you understand sampling for both qualitative and quantitative research.

Let’s start with first stage, the target or theoretical population.

‍

The Theoretical (Target) Population/Segment, N

The theoretical population or segment represents every person you're currently trying to understand, study, or affect. It's more conceptual than literal because you can't study everyone. As mentioned in Topic 1 of this handbook, it can be challenging to clearly define who your target or ideal population is.

Even if you can define your population or segment, it’ll never be accessible. People are constantly changing. At any given point in time, yes, there’s a discrete number of people that fit your population/segment and MIP definitions. But as time goes on, new people will fit those definitions, while others will become less relevant and informative. While you can’t study your entire population, you can access and recruit participants from a sampling frame.

‍

Sampling Frame (the Accessible Population)

The accessible population is everyone you can contact for a study at any given moment. This accessible population is represented in a sampling frame. The sampling frame is typically in a list or table format that contains potential participants. Each participant has a way to be contacted (like an email address) along with important, measured, and recorded variables (such as location, phone preference, primary language spoken, etc.).

For recruitment, you want an informative sampling frame. It should include the core variables that your stakeholders care about alongside useful information to help you figure out what a representative sample looks like.

The larger your sampling frame, the easier it’ll be to meet a desired sample or number of participants.

And you want your sampling frame to be large. The larger it is, the more likely it is that you'll get the desired or wanted participants in a reasonable amount of time. If you can, think about combining sampling frames from different sources. Check out this presentation on creating a research panel, an internal sampling frame that you create and maintain that’s filled with participants from important populations/segments.

Generalizations (or inferences from your sample back to your population) sadly can only be made back to your sampling frame, not the inaccessible, theoretical population/segment-of-interest. The idea of generalizations is covered more in Handbook 4, Topic 2.

‍

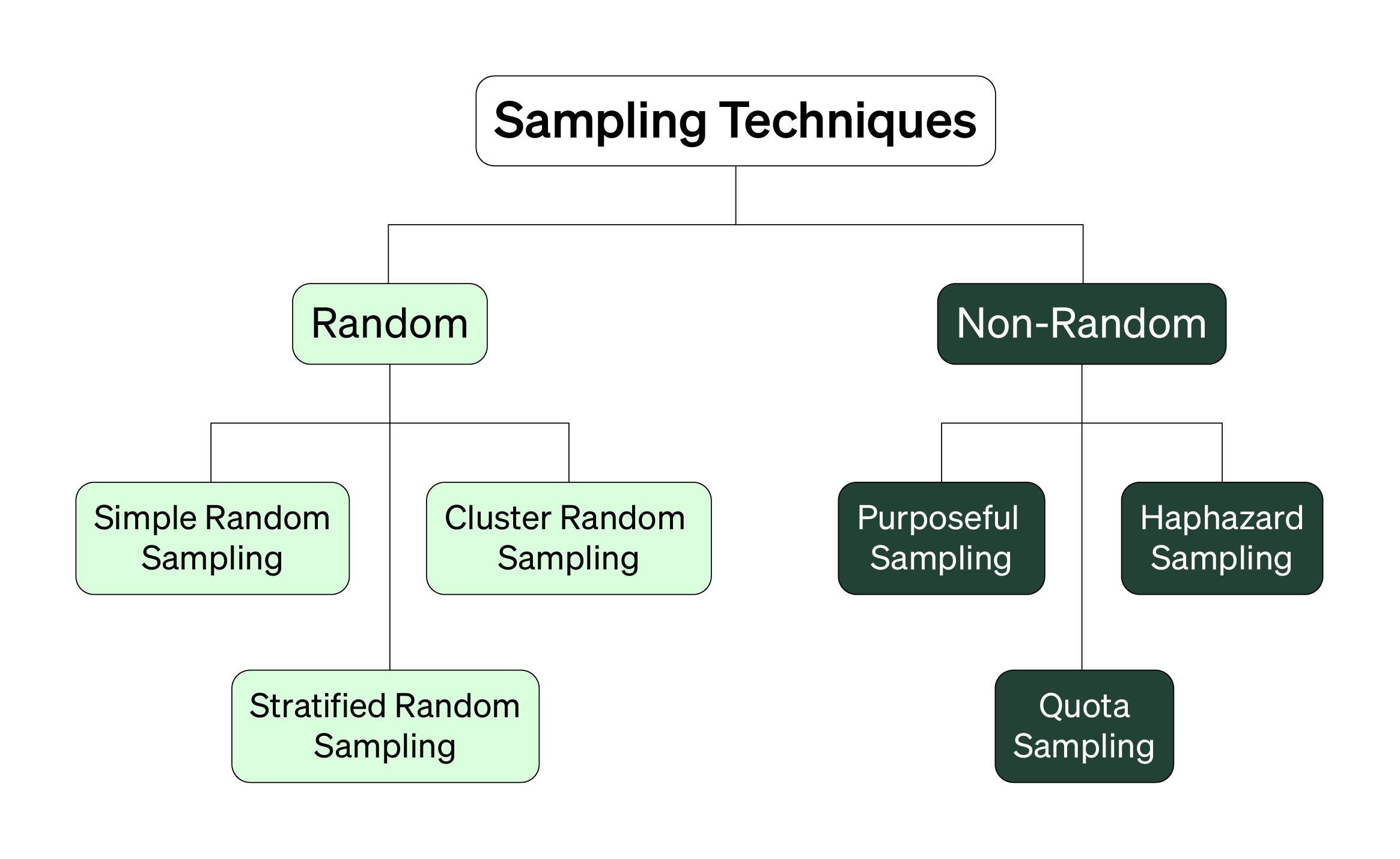
Sampling Techniques

You use a sampling technique to select a portion of your sampling frame for every study you run. There are two groups of sampling techniques: those that are random and those that are non-random. Check out Topic 3 and 4 in this handbook for more to learn more about when to use each.

‍

Sampling Pool

The sampling pool is the group of people you actually contact or recruit to participate in a research study. The number of people you contact is the denominator (or bottom number) when you calculate your response rate. For example, if you sent out a survey to 100 people (aka your sampling pool) and got 15 responses back (aka your sample), then your response rate would be 15%.

‍

Sample Size, n

The sample (or sample size) is the set final number of people that participated in your study. It's an observable, whole number commonly referred to as your sample size (denoted with a lowercase n). When you select people from your sampling frame, you probably have a desired or preferred sample size in mind. However, a desired sample sizes is easier to want than to actually get (an idea covered more in Handbook 4).

‍

The (Observable) Data Distribution

While data distributions isn’t an explicit stage when sampling, discussing it does serve as a bridge to other an abstract but important sampling ideas.

Let’s pretend that you had a sample size of 100 fruit survey respondents. In the survey, you ask every fruit one question: how many minutes a month do you dance? You graph your survey data to see the data distribution. The data distribution represents not only the range of answers for this one question but how many times each answer was given (also known as frequency). Your study data when graphed could result in many different shapes as shown below.

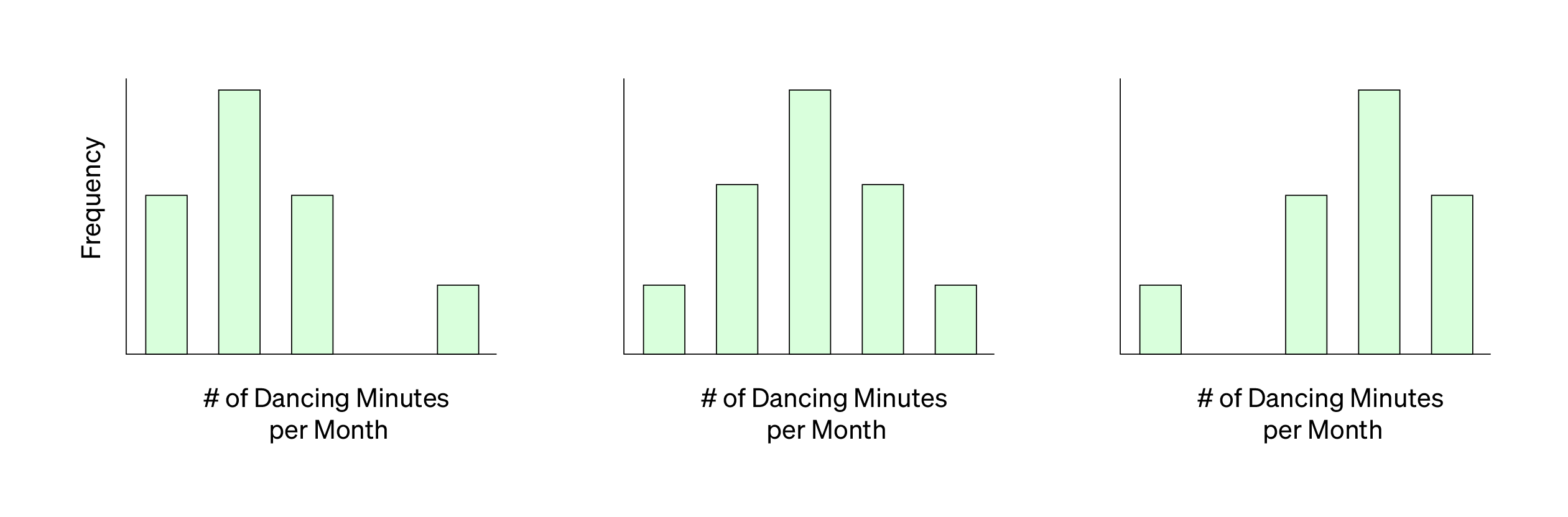
But this raises a problem: how do you know how well this specific group of 100 fruit survey respondents reflects what’s true about all fruits and their dancing habits? Even if your most of your data fell around 10 minutes a month, it doesn’t mean that the entire population of fruits dance about 10 minutes a month.

There’s a difference between the data distribution you see in your sample and what’s true at the population level.

To understand this means discussing something known as the sampling distribution of the mean. Check out this resource to learn more. In the search box below are some additional concepts to help expand on what’s covered here.

Recruiting participants can be a complex process. Sometimes, recruiting means using math and formulas. One of the most effective uses of math in recruiting is when you use random sampling.